海狸(Bebras)国际计算思维挑战由国际信息学奥林匹克竞赛前主席(International Olympiad in Informatics，缩写:I0I)、维尔纽斯大学数学与信息学研究所教授 Prof. Dr(HP)Valentina Dagienè于2004 年创立，它是一项面向全球青少年的计算思维与信息学教育活动，依照奥林匹克模式，各国主办方成为全球组委会成员，共同命题、共同投票选择年度题库全球评奖。旨在通过趣味性的题目激发学生对计算机科学的兴趣，在不需要掌握任何编程语言的前提下，培养他们用计算机和逻辑思维去解决问题的能力，是一项辅助学校 AI 教育的优质活动。
目前全球每年有 85 个国家和地区的 400 万学生参与，其中法国约 70 万学生参加，德国和英国分别约 50万和 40 万学生参加。Bebras 也受到了美国麻省理工学院、英国剑桥大学、加拿大滑铁卢大学等世界知名大学的官方认可和推荐。Bebras 的题目设计贴近生活，将抽象的信息学知识具体化，使未曾受过编程或机器人教育的学生也能利用逻辑、归纳、推理、运算等数学能力完成解题。
随着人工智能时代来临，计算思维作为嫁接数学与 AI、编程、机器人教育的重要桥梁，日益受到各国教育界重视。
热！2025年海狸（Bebras）国际计算思维挑战分数说明与解析
世界名校对海狸（Bebras）国际计算思维挑战的官方推荐
美国麻省理工学院 招生办公室 官方推荐
MIT Admissions
英国剑桥大学 计算机科学与技术系 官方推荐
University of Cambridge Department of Computer Science and Technology
加拿大滑铁卢大学 计算机科学学院 官方推荐
University of Waterloo Cheriton School of Computer Science
什么是计算思维？
海狸妹妹：HI~ 哥哥，什么是计算思维？
海狸哥哥：它是一种解决问题的思维模式。 举个例子，整理图书馆书籍，你会怎么做？
海狸妹妹：我会将书籍分类，然后放进书 柜，再把书柜摆整齐。
海狸哥哥：很好！计算思维非常重要的就是分解思维——把大问题拆小。 但还要解决书籍索引、摆放、查找等问题。
我们需要：
分解
把大问题分解成小问题来解决
摘要
提取关键要点（例如目录规则、布局特点）
建模
设计模式框架（布局→结构→设计）
算法设计
执行过程（方法→步骤→执行）
这一整套思维活动就是计算思维！它通过“分解 - 抽象 - 建模 - 算法设计”来高效解决问题，并能不断优化，是信息科技 学习的核心素养。
计算思维：
计算思维是指个体运用计算机科学领域的思想方法，在问题解决过程中涉及的抽象、分解、建模、算法设计等思维活动。
具备计算思维的学生，能对问题进行抽象、分解、建模，并通过设计算法形成解决方案；
能尝试模拟、仿真、验证解决问题的过程，反思、优化解决问题的方案，并将其迁移运用于解决其他问题。
摘选——信息科技课程标准（2022）
海狸哥哥：现在大家明白什么是计算思维了吧，那咱们 一起来思考一下下面的问题！
Bebras 真题
各国专家命题，汇聚 AI 教育全球智慧
Bebras 国际计算思维挑战的题目筛选是一个严谨的、多阶段协作的过程，结合了教育性和趣味性。以下是其题目产生和筛选的核心流程，涵盖国际协作和学术审校机制：
各国专家命题
每个Bebras成员国组织专家提供原创题目。
全球投票严选
Bebras全球组委会每年召集所有成员国代表和专家集中开会，从各国选题中投票选择年度最佳试题成为当年题库。
各国开展活动
各个成员国从该年度的国际题库中选择题目，用于自己国家的活动。
Bebras真题展示
青蛙与蚊子
等级A（1-2年级）
青蛙可以沿着蓝线从一片睡莲跳到另一片睡莲。它以如图所示的睡莲作为起点，每片睡莲只能跳跃一次，目标是到达蚊子所在的睡莲。
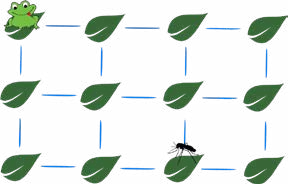
请问，如果青蛙只能精确地跳跃四次，它可以有多少种不同的路径到达蚊子所在的睡莲？
(A) 5 (B) 6 (C) 7 (D) 8
答案B
小怪兽
等级B（3-4年级）
小艾正在尝试学习小怪兽的外貌特征。她研究了以下五张小怪兽的照片，并记录了一些准确描述她所见的笔记。
然之，当小艾看到第六张小怪兽的照片时，她意识到她的一条笔记肯定是错误的。
小艾关于小怪兽的哪一条笔记肯定是错误的？
(A) 小怪兽都有牙齿
(B) 小怪兽有时有翅膀
(C) 小怪兽要么长角，要么有三只眼睛，但不会既长角又有三只眼睛
(D) 如果小怪兽恰好有两只手臂，那么也一定会有两只脚
答案D
按下按钮
等级C（5-6年级）
如图所示，保罗需要把球移动到储藏区，如果他按下 A、B 或 C 按钮中的一个，相应的门就会打开，正好有一个球落到储藏区。已知储藏区内球的数字标签必须按照由小到大的顺序排列，那么按照以下哪个序列按动按钮使得储藏区中的球数量最多？
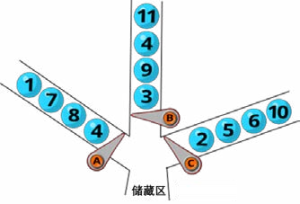
(A) CBACCBCAB (B) CBACCABC
(C) CBACABCC (D) CBABCCAC
答案B
解析：对于任务所示的球，正确的序列是 CBACCABC。存储区将包含标记为 [2, 3, 4, 5, 6, 8, 9, 10] 的球。下面介绍为什么无法将超过 8 个球放入存储区。保罗还可以观察左侧区域（带有按钮 A）、中间区域（B）或右侧区域（C）的球，找出球标签所构成一个递增子序列。在左侧区域，有一个递增子序列 [4, 8]。在中间区域，递增子序列是 [3, 9]，而在右侧区域的递增子序列是 [2, 5, 6, 10]。我们可以将这 8 个球移动到存储区。所有其他选项都会导致存储区中的球序列不是递增的。
计算思维相关知识：
数组
数组指的是一种数据结构，它会在连续的内存区域存储多个相同类型的元素。通过索引，能快速访问数组中的任意元素。
归并
在计算机科学和数学中是一种重要的操作，核心思想是将 两个或多个有序序列 合并成一个新的有序序列。其关键在于利用已有序列的有序性，通过比较和移动元素来高效完成合并，避免重复排序，从而提升效率。
计数
等级D（初中及以上）
米娅喜欢每晚住宿地点不同的徒步旅行。下图展示了她下一个假期正在考虑的徒步路线。米娅 每天只能走一到两个路段（由虚线标记）。图中显示了起点、终点以及她可以停留过夜的所有地点。图中展示了两种可能的路线：
路线 1 有 3 个过夜点。
路线 2 有 4 个过夜点。
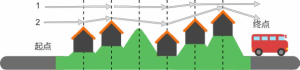
包括示例的两条路线，米娅在她的徒步假期中可以选择多少种不同的路线？
(A) 2 (B) 4 (C) 6 (D) 8
答案C
解析：
包括示例的两条路线，米娅在她的徒步假期中可以选择6种不同的路线。
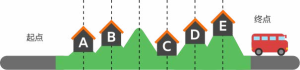
我们可以通过分解问题来解决这个问题：首先我们注意到 Mia 必须在 B 和 C 停留，因为这两地之间的距离是她一天能走的最远距离。这让我们可以将到达这两点之前和之后的路段视为两个小问题。可以看出从起点到 B 有两种方式（分别展示在路线 1 和路线2 中）。因此，到达 C 的路线只有两种。现在我们看看从 C 到终点有几种方式。在这个较小的问题中，可以找出只有三种可能性：
C → D → E → 终点
C → E → 终点
C → D → 终点
这意味着总共有 2×3=6 种可能的路线。
在这种情况下，任务可以通过分解成两个较小的问题来解决。对于类似的更大问题，会使用动态编程方法。这是一种策略，算法通过将问题分解成非常小的问题，并利用这些小问题的解决方案来构建更大的解决方案。
如果你将可以到达的地点编号为起点，A，B，C，D，E，终点，你可以制作一个表来显示到达每个地点的方法数目。
| 地点 | 到达的路线数 |
| 起点 | 1 |
| A | 1（直接从起点） |
| B | 1+1=2（从起点或A出发） |
| C | 2（必须从B出发） |
| D | 2（必须从C出发） |
| E | 2+2=4（从C或从D出发） |
| 终点 | 2+4=6（从D出发或从E出发） |
首先，我们从房屋、山脉和公交车的具体细节中抽象出来，仅给它们标上标签。
然后算法开始解决小问题；从起点开始，有多少种方式可以到达每个点。
这是一种策略，如果我们知道到达 'B' 点的答案，就可以容易地计算出到达 'C' 点的答案。
以这种方式填写上述表格被称为动态规划。这是一种智能算法，用于在类似情况下找到解决方案，也适用于更大的问题，人类要解决这些问题会特别耗时。
如需更多题目，可扫码领取⇓
